Exact probabilities for the indeterminacy of complex networks as perceived through press perturbations

Abstract

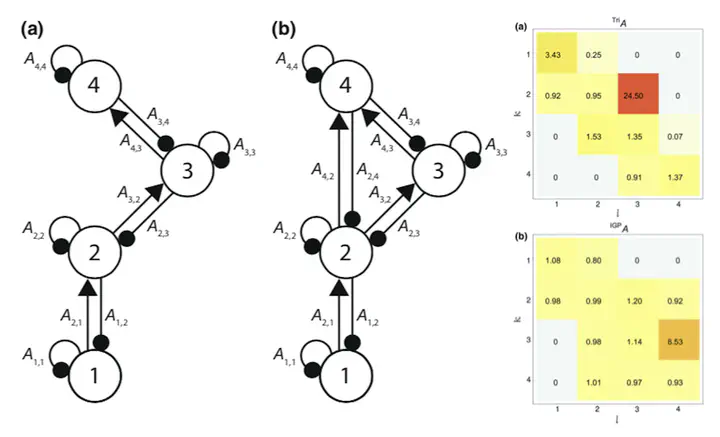
We consider the goal of predicting how complex networks respond to chronic (press) perturbations when characterizations of their network topology and interaction strengths are associated with uncertainty. Our primary result is the derivation of exact formulas for the expected number and probability of qualitatively incorrect predictions about a system’s responses under uncertainties drawn form arbitrary distributions of error. Additional indices provide new tools for identifying which links in a network are most qualitatively and quantitatively sensitive to error, and for determining the volume of errors within which predictions will remain qualitatively determinate (i.e. sign insensitive). Together with recent advances in the empirical characterization of uncertainty in networks, these tools bridge a way towards probabilistic predictions of network dynamics.