Geometric complexity and the information-theoretic comparison of functional-response models
Abstract
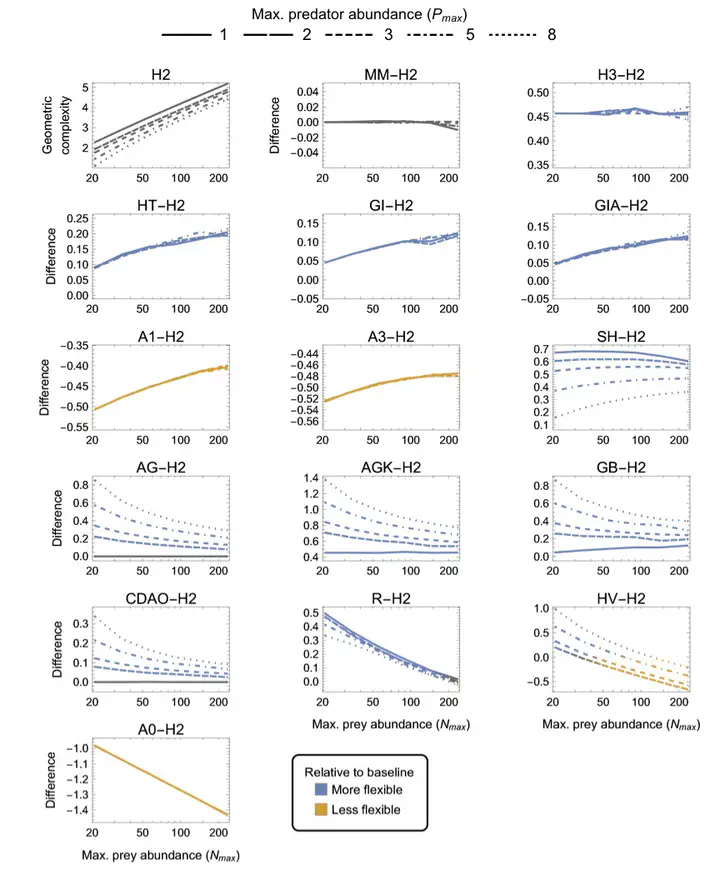
The assessment of relative model performance using information criteria like AIC and BIC has become routine among functional-response studies, reflecting trends in the broader ecological literature. Such information criteria allow comparison across diverse models because they penalize each model’s fit by its parametric complexity — in terms of their number of free parameters — which allows simpler models to outperform similarly fitting models of higher parametric complexity. However, criteria like AIC and BIC do not consider an additional form of model complexity, referred to as geometric complexity, which relates specifically to the mathematical form of the model. Models of equivalent parametric complexity can differ in their geometric complexity and thereby in their ability to flexibly fit data. Here we use the Fisher Information Approximation criterion to compare, explain, and contextualize how geometric complexity varies across a large compilation of single-prey functional-response models — including prey-, ratio-, and predator-dependent formulations — reflecting varying levels of phenomenological generality and varying apparent degrees and forms of non-linearity. Because a model’s geometric complexity varies with the data’s underlying experimental design, we also sought to determine which designs are best at leveling the playing field among functional-response models. Our analyses illustrate (1) the large differences in geometric complexity that exist among functional-response models, (2) there is no experimental design that can minimize these differences across all models, and (3) even the qualitative nature by which some models are more or less flexible than others is reversed by changes in experimental design. Failure to appreciate geometric complexity in the empirical evaluation of functional-response models may therefore lead to biased inferences for predator-prey ecology, particularly at low experimental sample sizes where the relative effects of geometric complexity are strongest. We conclude by discussing the statistical and epistemological challenges that geometric complexity poses for the study of functional responses as it relates to the attainment of biological truth and predictive ability.